PDE are working with smooth functions, defined in some region. In grid methods the region of continual changing of arguments, where we look for a solution of PDE, is replaced by a calculation grid – finite discrete set of points, connected by non-intersecting line. The calculation grid may be treated as subdivision of the region on small sells. In finite-differences methods and finite-elements methods we are looking for a solution in the nodes of the grid, in finite-volume methods – we look for a solution in the “centers” of cells.
Thus, in grid methods instead of looking for a solution as an unknown function u(x,y,z) we are looking for a set u = (uj) containing the values of this function in the nodes of a grid.
Calculation grid is regular, if there is isomorphic transform of this grid on rectangular grid of a unit cube (grids а and б on the next figure).
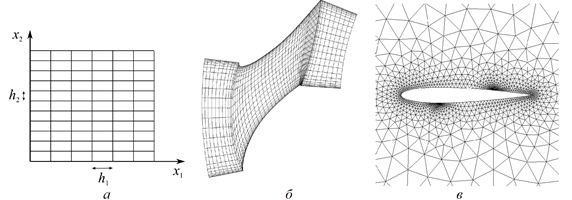
Regular grids may be uniform (constant step of a grid) and non-uniform. Regular grids may be divided on rectangular (grid а) and curvilinear (grid б).
All other grids are referred as irregular (grid в on the figure above).
The advantage of regular grids is in more accurate approximation of derivatives. However, such grids are difficult to construct in regions with complicated geometries.
The main advantage of irregular grids is that they are easy to be constructed in regions with arbitrary geometry. However, we are to pay for this by a lower accuracy of solution.
-
Finite differences methods
Finite difference method (FDM) is the most natural approach to discretization of PDE.
Learn more… -
Finite element methods
Finite elements method (FEM) is the most popular approach in all commercial CAE applications. It uses irregular meshes.
Learn more… -
Finite volume methods
Finite volume method (FVM) is another universal method to be used for irregular grids.
Learn more…
In commercial applications FEM and FVM are dominated.
In commercial CFD software about 80% of application use FVM and about 15% of application use FEM.
In solid mechanics the proportion is opposite - about 80% of application use FEM and about 15% of application use FEM.
Other approaches (FDM is among them) is used by 5% of commercial applications.
Back to Technology page…
