Elliptic PDEs are usually associated with steady-state problems.
The simplest example of an elliptic PDE (let it be 2-dimensional) is the Laplace’s equation,
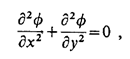
which governs incompressible, potential flow (or field).
If we’ll set on the square 0≤x≤1, 0≤y≤1 boundary conditions
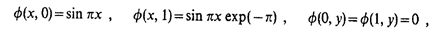
then the Laplace’s equation will have the following exact solution:
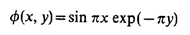
If in the right side of the equation we have not the zero but some function f(x, y), then such an equation is called Poisson equation – it is elliptic as well.
As an example of Poisson equation one can give, for instance, the equation for electric field potential – in this case the right hand function f(x, y) of the equation is the distribution of electrical charges in the given region, and the unknown function ɸ(x, y) is the potential of electric field.
Poisson equation for the stream function in two-dimensional rotational flow is an elliptic PDE.
The steady Navier-Stokes equations are also elliptic.
A lot of examples of elliptic PDE one can obtain in classical mechanics from equations responsible for energy preservation.
Elliptic equations one can find also in quantum mechanics – for instance, steady Schrodinger equation.
For second-order elliptic PDE an important maximum principal exist. Namely, both the maximum and minimum values of ɸ must occur on the boundary (except the trivial case that ɸ is a constant).
The maximum principle is useful in testing that computational solutions of elliptic PDEs are behaving properly.
Go to this page for more detailed discussion of elliptic problems.
